라즈이노 iOT

【 프로세싱 기초#25】 좌표 트랜스폼 이용한 도형 그리기

 직교좌표계 위에 원이나 사각형 등의 도형을 여러 개를 그려야 할 때가 있을 것이다.  이 때 도형들의 상대적인 간격을 감안하여 좌표를 계산해서 그릴텐데, 이는 코딩을 할 때 많이 헷갈릴 수 있는 부분이 된다.  그래서 이럴 때 사용할 수 있는 좌표관련 함수가 바로 translate() 함수이다. 기준점 좌표를 마음대로 옮길 수 있는 함수로서 옮기기 직전의 좌표 기억 하는 함수인 pushMatrix()와 기억된 좌표를 다시 불러내는 popMatrix()함수를 함께 사용한다면, 직교좌표계 위에서 보다 손 쉽게 여러개의 도형을 그려낼 수 있게 된다.  오늘은 이와 관련하여 다루어 보고자 한다.

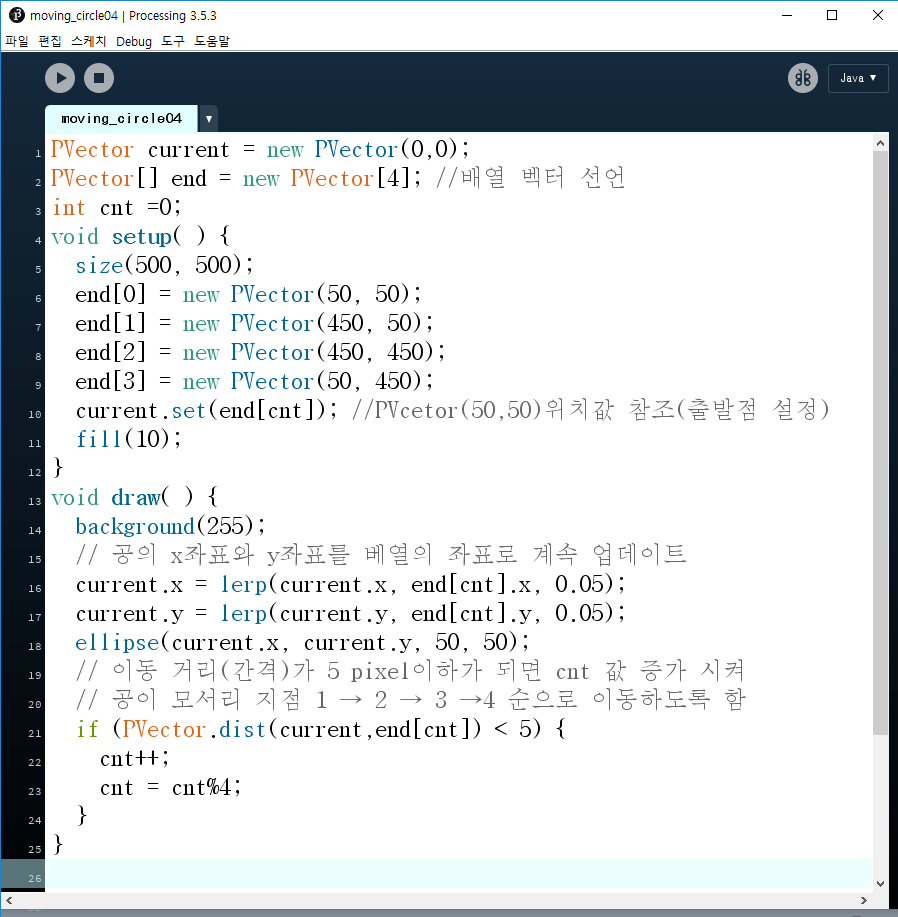
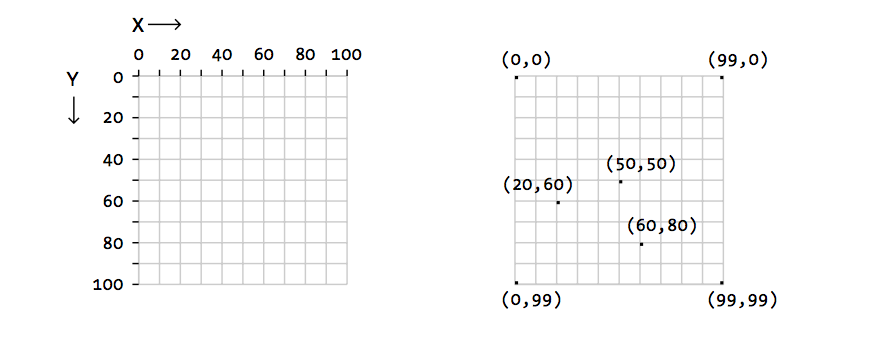
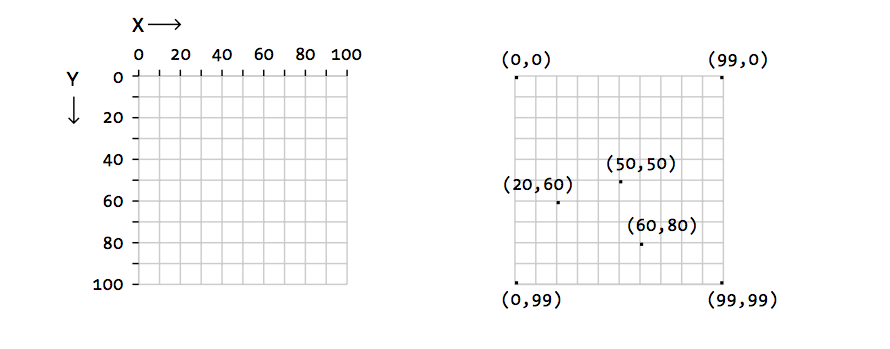
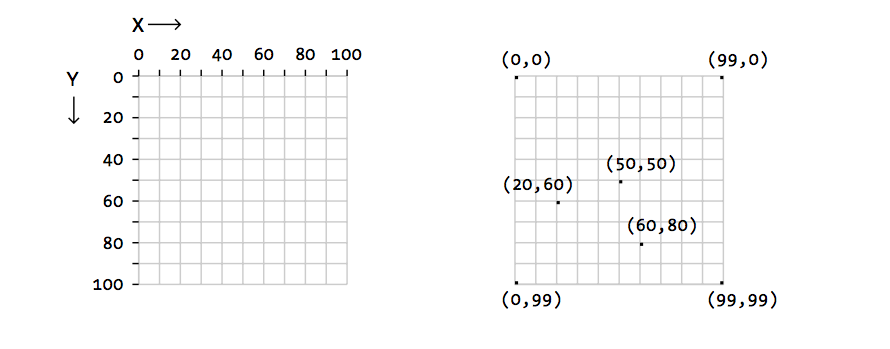
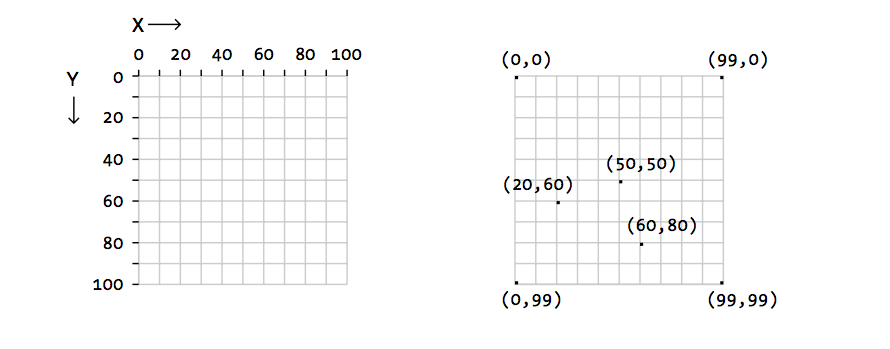
[ 프로세싱의 화면 좌표 ]  - 100 x 100 pixel 예시 

▶ 문제  :  아래 실행결과 이미지 처럼 하우스1 도형들을 그리고, 추가적으로 변환함수(translate(x,y))를 이용하여 house2를 그려라.

  [ 조건(hint) ]

   1. 화면 사이즈(가로x세로 픽셀) : 600 x 450 
   2. 배경색 및 라인: background(255), 하우스 1(삼각형:fill(0), 사각형:fill(100)) , 하우스2(삼각형:fill(200, 50, 0) , (사각형 : fill(50, 100, 200) )   
   3. house1 사용자 함수와 house2 사용자 함수 각각 만들어 사용.  (인자값 : int x, int y)

   4. house2는 좌표축 자체를 움직여 주는 translate() 함수를 사용하여 그릴 것 (pushMatrix(), popMatrix() 함께 사용)

  [참고]

 1. translate(x,y) 함수는 좌표축 자체를 x,y의 위치로 이동해주며, 그 위치가 옮겨진 축의 0,0의 위치가 된다. 

    ex) - rect(0, 0, 100, 100)  : 0, 0의 위치에 100x100 크기의 사각형을 그린다. 

        - translate(200,200) : 원점이 200, 200 위치로 옮겨진다.(상대적으로) 

        - rect(0, 0, 100, 100) : 원점이 옮겨 졌기 때문에 사각형이 겹쳐서 그려지지 않는다. 

        [ 사각형 그리기 함수 : rect(x, y, width, height) ]

 2. pushMatrix()  & popMatrix() 함수를 활용하라

  translate() 함수를 이용하여 코딩 할 때 경우에 따라 특정 구간만 원점 좌표를 이동시켜 계산 후 , 다시 원래의 원점 좌표값으로 되돌아 오면 편한 경우가 있다. 이럴 때 (옮겨진)현재의 좌표를 기억 시켜두는 함수
[ pushMatrix())와 다시 그 좌표 값을 꺼내는 함수(popMatrix()) 를 이용하면 코딩이(좌표값 계산) 수월해질 수 있다. ]

▶ 문제 (실행결과) 
아래처럼 동작되도록 코딩하라.

- 지붕(삼각형 함수 사용: triangle(x1, y1, x2, y2, x3, y3)

- 집몸체(사각형 함수 사용 : rect(x, y, width, height)

같은 모양의 도형 반복이므로 for 반복문을 활용하여 간략화 하라.

- house 1은 translate()함수 없이 그려보고, house 2를 그릴 때 translate()함수와 pushMatrix(),popMatrix()함수를 활용하여 그려 보아라.

▶ 프로그램(code) : 
(이미지를 클릭하면 확대 됩니다)

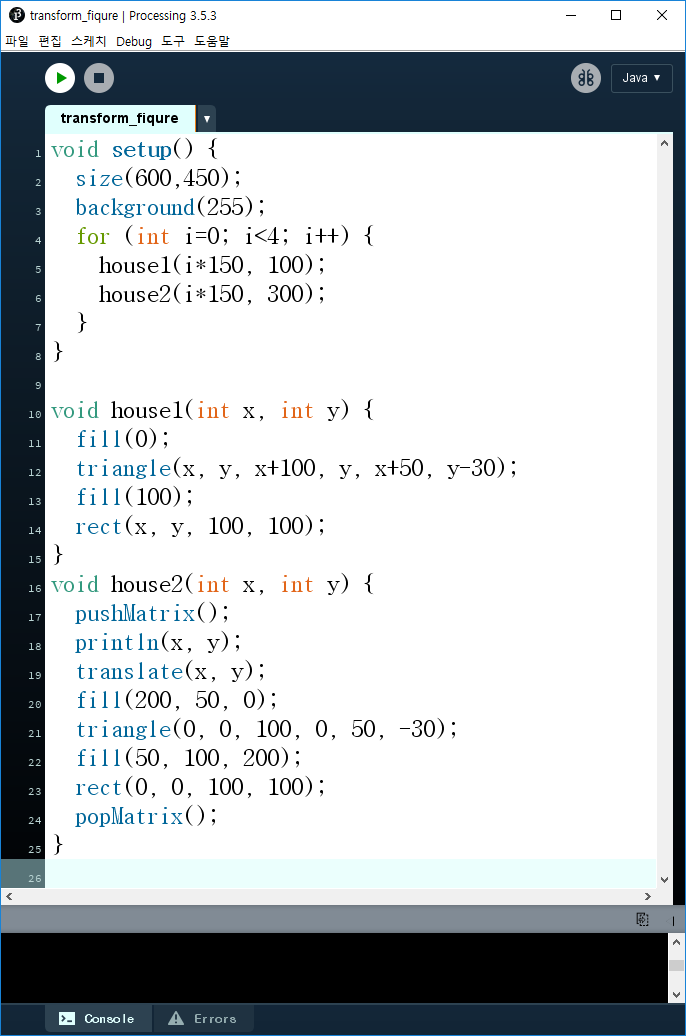
void setup() {
  size(600,450);
  background(255);  
  for (int i=0; i<4; i++) {
    house1(i*150, 100);
    house2(i*150, 300);    
  }
}

void house1(int x, int y) {
  fill(0);
  triangle(x, y, x+100, y, x+50, y-30);
  fill(100);
  rect(x, y, 100, 100);
}
void house2(int x, int y) {
  pushMatrix();
  println(x, y);
  translate(x, y);
  fill(200, 50, 0);
  triangle(0, 0, 100, 0, 50, -30);
  fill(50, 100, 200);
  rect(0, 0, 100, 100);
  popMatrix();
}

▶ 프로그램(code) 다운로드: 
(압축 파일을 풀어서 사용하세요)

【 프로세싱 기초#24】 화면 4구석을 감속 회전하는 공 표현하기

 지난 시간 원(공)이 출발지점부터 목표지점까지 움직일 때 감속하여 움직이도록 표현하였다. 이번에는 화면의 4군데 모서리 부분을 감속 이동으로 반복 회전 시켜 보자.

[ 프로세싱의 화면 좌표 ]  - 100 x 100 pixel 예시 

▶ 문제  :  크기(50x50 pixel) 원을 목표 지점(400,400)까지 움직이되 서서히 감속시켜라.

   [ 조건 :  1. 화면 사이즈(가로x세로 픽셀) : 500 x 500) , 
              2. 배경색 및 라인: background(255), 원 내부 채움색( fill(10) )
              3. 선형 보간 함수 사용 : lerp(a, b, t) -변수 a의 값에서 b의 값까지 t값 비율 만큼 변경한 값을 반환 함

              4. 이동 목표지점(4 곳 모서리 부분)을 배열 벡터로 선언 , 'PVector[] end = new PVector[4]' ]

[참고]

 1. 선형 보간법: 출발점과 끝점을 알고 있을 때, 그 사이에 위치한 값을 추정하기 위하여 직선 거리에 따라 선형적으로 계산하는 방법

 2. 선형보간 함수의 계산 식 : 함수 lerp(a, b, t)는 내부적 다음과 같은 식으로 계산된다.

   function lerp(a, b, t)

       return a * (1-t) + (b*t)

   end

<감속이 어떻게 이루어 지는 것인지 값을 확인>

[ ※ 참고, 선형보간 함수의 계산 식 : 함수 lerp(a, b, t)는 내부적 다음과 같은 식으로 계산된다.

위, 첫 번째 x와 두 번째 x의 차이값(위치)과 두 번째 x와 세 번째 x 차이값을 비교해 보면,  루프를 돌수록 점점 줄어 드는 것을 확인 할 수 있다. y값도 마찬가지.  따라서 루틴을 돌 수록 공이 움직이는 위치가 점점 짧아 지게 됨으로 공이 감속하여 움직이는 것을 볼 수 있는 것이다.  
 그리고 t 값을 조절하면 감속되는 속도를 조절 할 수 있다.

▶ 문제 (실행결과) 
아래처럼 동작되도록 코딩하라.

화면 사이즈(pixel) [ 500 x 500 ]

목표 지점 위치 [ (x, y) : A(50, 50) , B(450, 50) , C(450, 450) , D(50, 450) ]   

[실행결과 영상]

▶ 프로그램(code) : 
(이미지를 클릭하면 확대 됩니다)

PVector current = new PVector(0,0);
PVector[] end = new PVector[4]; //배열 벡터 선언
int cnt =0;
void setup( ) { 
  size(500, 500);
  end[0] = new PVector(50, 50);
  end[1] = new PVector(450, 50);
  end[2] = new PVector(450, 450);
  end[3] = new PVector(50, 450);
  current.set(end[cnt]);  //PVcetor(50,50)위치값 참조(출발점 설정)   
  fill(10);
} 
void draw( ) { 
  background(255);
  // 공의 x좌표와 y좌표를 베열의 좌표로 계속 업데이트
  current.x = lerp(current.x, end[cnt].x, 0.05);  
  current.y = lerp(current.y, end[cnt].y, 0.05);
  ellipse(current.x, current.y, 50, 50);
  // 이동 거리(간격)가 5 pixel이하가 되면 cnt 값 증가 시켜
  // 공이 모서리 지점 1 → 2 → 3 →4 순으로 이동하도록 함 
  if (PVector.dist(current, end[cnt] ) < 5) {
    cnt++;
    cnt = cnt%4;  // 나머지 연산자를 사용하여 0, 1, 2, 3 값을 반복
  }  
}

▶ 프로그램(code) 다운로드: 
(압축 파일을 풀어서 사용하세요)

【 프로세싱 기초#23】 감속하는 공 표현하기 (가속도 적용 - 움직이는 원3)

 지난 시간 PVecter 자료형에 대해 다루어 보았다. 이번 시간부터는 이 벡터 자료형을 본격적으로 활용해볼 텐데, 오늘은 원(공)이 출발지점부터 목표지점까지 움직일 때 목표점에 도달할 수록 가속도가 줄어 들어 서서히 도달 하는 듯한 움직임을 나타내보려 한다. 
(참고, 이런 형태는 게임등에서 많이 활용되는 기법으로 유니티(unity) 등에서 선형보간 함수(기법)를 이용해서 구현하게 된다. )

[ 프로세싱의 화면 좌표 ]  - 100 x 100 pixel 예시 

▶ 문제  :  크기(50x50 pixel) 원을 목표 지점(400,400)까지 움직이되 서서히 감속시켜라.

   [ 조건 :  1. 화면 사이즈(가로x세로 픽셀) : 500 x 500) , 
              2. 배경색 및 라인: background(255), 원 내부 채움색( fill(10) )
              3. 선형 보간 함수 사용 : lerp(a, b, t) -변수 a의 값에서 b의 값까지 t값 비율 만큼 변경한 값을 반환 함 ]

[참고]

 1. 선형 보간법: 출발점과 끝점을 알고 있을 때, 그 사이에 위치한 값을 추정하기 위하여 직선 거리에 따라 선형적으로 계산하는 방법

 2. 선형보간 함수의 계산 식 : 함수 lerp(a, b, t)는 내부적 다음과 같은 식으로 계산된다.

   function lerp(a, b, t)

       return a * (1-t) + (b*t)

   end

▶ 문제 (실행결과) 
아래처럼 동작되도록 코딩하라.

[실행결과 영상]

▶ 프로그램(code) : 
(이미지를 클릭하면 확대 됩니다)

PVector begin, end, current;  // PVector 변수 선언
void setup( ) { 
  size(500, 500);
  begin = new PVector(0, 0);  // 원의 출발점
  end = new PVector(400, 400);   // 원의 도착점
  current = begin;    //참조형 변수, 현재의 위치를 일치시킴(업데이트)
  fill(10);
} 
void draw( ) { 
  background(255);
  current.x = lerp(current.x, end.x, 0.05);  
  current.y = lerp(current.y, end.y, 0.05);
//  println("x=",current.x);    // x 값의 감속 확인용 
//  println("y=",current.y);    // y 값의 감속 확인용 
  ellipse(current.x, current.y, 50, 50);  
}

<감속이 어떻게 이루어 지는 것인지 값을 확인>

[ ※ 참고, 선형보간 함수의 계산 식 : 함수 lerp(a, b, t)는 내부적 다음과 같은 식으로 계산된다.

   function lerp(a, b, t)

       return a * (1-t) + (b*t)

   end    ]
위, 첫 번째 x와 두 번째 x의 차이값(위치)과 두 번째 x와 세 번째 x 차이값을 비교해 보면,  루프를 돌수록 점점 줄어 드는 것을 확인 할 수 있다. y값도 마찬가지.  따라서 루틴을 돌 수록 공이 움직이는 위치가 점점 짧아 지게 됨으로 공이 감속하여 움직이는 것을 볼 수 있는 것이다. 
 그리고 t 값을 조절하면 감속되는 속도를 조절 할 수 있다.

▶ 프로그램(code) 다운로드: 
(압축 파일을 풀어서 사용하세요)

【 프로세싱 기초#22 】 PVector 자료형 활용하여 도형 그리기

 프로세싱 초기에 직선, 타원, 삼각형을 그려주는 함수에 직접 숫자를 입력하여 도형들을 그려보았다.  이번에는 PVector 자료형을 이용하여 그려보려한다.  이를 통해 PVector 자료형 활용하는 법에 대해 충분히 익힐 수 있을 것이다. 
 int, float 자료형을 기본자료형이라하고, 새롭게 등장한 PVecter 자료형은 백터 형태의 좌표를 활용할 수 있는 자료형입니다. 벡터 자료형을 사용하면, 예를 들어 움직이는 도형을 구현 할 때, 서서히 혹은 빨리 움직이고 멈추게 하는 등의 가속도를 쉽게 구현 할 수 있다.    

(참고 :  '스칼라' 와 '벡터'의 차이를 이해하면 좋은데, 스칼라는 크기만을 나타내는 물리량이지만,  벡터는 크기와 방향성을 동시에 나타낼 수 있는 물리량이다.  따라서 int, float 등은 크기값 만을 표시할 수 있는 '스칼라' 자료형 이지만, PVector는 속도, 가속도, 힘, 운동량 등을 구현해 줄 수 있는 '벡터' 자료형이다.)

[ 프로세싱의 화면 좌표 ]  - 100 x 100 pixel 예시 

▶ 문제  :  아래 실행 결과 화면을 PVector 자료형을 선언하여 아래 각각의 도형을 나타내어라. 

   [ 조건 :  1. 화면 사이즈(가로x세로 픽셀) : 500 x 500) , 
              2. 배경색 및 라인: background(255), strokeWeight(10)
              3. 직선, 점, 삼각형, 사각형, 타원, 호 그리기 함수, 각각 사용  ]

[참고]

 1. 점 그리기 :  point(x, y);   

 2. 선분 그리기 : line(start x, start y, end x, end y);

 3. 삼각형 그리기 : triangle(x1, y1, x2, y2, x3, y3); // 각각 세 꼭지점의 좌표

 4. 직사각형 그리기 : rect( x, y, width, height);  // x, y는 사각형 왼쪽 상단의 좌표

 5. 타원 그리기 : ellipse(center x, center y, width, height);

 6. 호 그리기 : arc(center x, center y, width, height, start angle, end angle);

▶ 문제 (실행결과) 
아래처럼 동작되도록 코딩하라.

▶ 프로그램(code) : 
(이미지를 클릭하면 확대 됩니다)

int diam = 10;           // 원의 직경 변수 선언(초기값 10 pixel)
float centerX, 

PVector v1, v2, k1, k2;   // PVector 선언
void setup( ) {
  size (500, 500);
  v1 = new PVector(30, 50);    // PVector(v1.x , v1.y)
  v2 = new PVector(width, height);  // PVector(v2.x , v2.y)
  k1 = new PVector(50, 100);   // PVector(k1.x , k1.y)
  k2 = new PVector(100, 200);  // PVector(k2.x , k2.y)
  strokeWeight(10);   // 선 굵기 (pixel)
}
void draw( ) {
  noLoop();       // 루프를 반복하지 않음
  background(255);
  line (v1.x, v1.y, v2.x, v2.y); //v1과 v2의 좌표값을 이용한 선 긋기
  point(v1.x+300, k1.x*2);   // 점을 찍을 때 위치: (330, 100) 
  //삼각형 세 꼭지점 triangle(x1, y1, x2, y2, x3, y3)
  triangle(v1.x+170, v1.y, k1.x+200, k1.y, k1.x+k2.x, k2.y-100);   
  // 직사각형 그리기 rect(x, y, width, height) 
  rect(k1.x, k2.y, width/3, height/3);     
  // 타원그리기 ellipse(center x, center y, width, height);
  ellipse(k2.x+200, k2.y+100, k1.y, height/4);
  // 호그리기 arc(center x, center y, width, height, start_angle, end_angle) 
  arc(250,400, 100,100, radians(0), radians(180));
  k2.add(k1);     // k2에 k1의 벡터 좌표를 더하라~! k2=(100+50, 200+100)
  arc(k2.x, k2.y, 100,100, radians(0), radians(v1.x+v1.y+k1.y));
}

▶ 프로그램(code) 다운로드: 
(압축 파일을 풀어서 사용하세요)

※ 다음 시간에 도형에 가속도를 적용해 보면, 좀 더 흥미가 생길 것이다. 

【 프로세싱 기초#21 】 빗방울 효과 내기 (10개의 커지는 원 구현)

 지난시간 원 하나를 화면 사이즈 만큼 키워 보았다. 이 원리를 이용해서 10개의 원을 랜덤으로 생성시켜 커지도록 해보려 한다. 마치 빗방울이 잔잔한 수면위에 퍼지는 듯한 멋진 효과를 구현해볼 수 있을 것이다. 

[ 프로세싱의 화면 좌표 ]  - 100 x 100 pixel 예시 

▶ 문제  :  화면에 10개의 원을 랜덤(크기와 위치)으로 생성 시켜 점점 커지도록 구현 하라.

   [ 조건 :  1. 화면 사이즈(가로x세로 픽셀) : 500 x 500) , 
              2. 배경색 및 라인: background(200), stroke(0), strokeWeight(3), fill(255, 10)
              3. 10개의 원은 배열과 반복문(for문)을 이용하여 간단히 구현할 것.
              4. 원 그리기는 ellipse(x, y, diam, diam) 함수 사용  ]

▶ 문제 (실행결과) 
아래처럼 동작되도록 코딩하라.

▶ 프로그램(code) : 
(이미지를 클릭하면 확대 됩니다)

int [] arrayOfDiam;         // 원의 지름값을 위한 배열 선언 (arrayOfDiam)
float [] arrayOfCentX, arrayOfCentY;    // 원의 중심 좌표를 위한 배열 (X , Y) 선언
void setup() { 
  size(500, 500);     //   출력 화면 크기 
  background(200);   //  배경화면 값 
  arrayOfDiam = new int[10];   //   10개의 원을 위한 배열 변수 생성
  arrayOfCentX = new float[10];   // 10개의 원을 위한 배열 변수 생성
  arrayOfCentY = new float[10]; // 10개의 원을 위한 배열 변수 생성
  for (int i=0; i<10; i++) {                      // 10개의 원,  for 반복문 사용
    arrayOfDiam[i] = int(random(500));   // 원의 배열 변수 값들에 초기값(랜덤)을 지정
    arrayOfCentX[i] = random(500); 
    arrayOfCentY[i] = random(500); 
  } 
  stroke(0);               //   선의 색,  굵기, 채우기 설정 
  strokeWeight(3);                    // 
  fill(255, 10);                            // 
} 
void draw() { 
  background(200);   // 
  for(int i=0; i<10; i++) {      //  원그리기 함수와 반복문을 이용해 랜덤으로 원을 그리기
    ellipse(arrayOfCentX[i], arrayOfCentY[i], arrayOfDiam[i], arrayOfDiam[i]); 
    arrayOfDiam[i] +=2;   //  원의 직경 증가 값 (pixel) 
    arrayOfDiam[i] %= width;   //  직경이 화면 폭(width)과 같아지면 나머지값(0) 을 넣어 리셋
  } 
}

▶ 프로그램(code) 다운로드: 
(압축 파일을 풀어서 사용하세요)

▶ 내용설명&실행결과(영상) :
(영상을 확대하고 고화질로 보세요)

(유튜브에서 보기  : 1080p 지원)

https://youtu.be/cYJt96xzHVk

( 카카오 : 720P 화질 지원)

【 Processing Basic#2 】 'The Circle grows' by Processing!

Let's implement a 10 pixel diameter circle. In fact, one circle does not grow, but it can be processed as visually that way.

▶ The Goal  : 
 Implement 10 pixels in the middle of the screen so that the circle grows to the screen size.

1. Screen size (width x height pixels): 500 x 500)

2. Background color and lines: background (180), stroke (0), strokeWeight (5), fill (255, 20)

3. Circle drawing uses ellipse (x, y, diam, diam) function

▶ Coding result :

▶ Coding and annotation : 

int diam = 10;           // Declaration of circle diameter variable (initial value 10 pixels)
float centerX, centerY;  // Declaring a circle's center point variable

void setup() { 
  size(500, 500); 
  centerX = width/2;     // Centering the center of the screen (width)
  centerY = height/2;    // Centering the center of the screen (height)
  stroke(0);           
  strokeWeight(5);       // Thickness of line
  fill(255, 20);   // The color of the border of the circle (255) and the transparency of the internal fill (Alpha: 20)
} 
void draw() { 
  background(180);     // To prevent afterimage
  ellipse(centerX, centerY, diam, diam); 
  diam += 10;          // Increase diameter by 10 pixels
  if (diam == width) diam = 0;   // Resets the maximum size of the circle so that it does not exceed the screen size
//  diam %= width;   // When the maximum size of the circle = screen size, the remaining value (%) becomes zero.
  delay(50);             // Time delay that the circle grows
}

▶ Code Download :

▶ Video lecture :  
(Look in full screen view at 1080P)

https://youtu.be/xZo5iQvQXOI

【 프로세싱 기초#20 】 점점 커지는 원 그리기

 지난시간 10개의 선을 랜덤생성시켜 움직이는 것처럼 구현해 보았다. 
이번 시간은 직경 10픽셀의 원이 점점 커지도록 구현해보려 한다.  실제로 하나의 원이 커지는 것은 아니지만 시각적으로 그렇게 보이도록 프로세싱으로 처리할 수 있다.   내용이 길지 않으므로 차근 차근 따라해보면 어렵지 않게 이해 할 수 있을 것이다.

[ 프로세싱의 화면 좌표 ]  - 100 x 100 pixel 예시 

▶ 문제  :  화면 가운데 10픽셀의 원이 화면 사이즈 까지 점점 커지도록 구현 하라. 

   [ 조건 :  1. 화면 사이즈(가로x세로 픽셀) : 500 x 500) , 
              2. 배경색 및 라인: background(180), stroke(0), strokeWeight(5), fill(255, 20)
              3. 원 그리기는 ellipse(x, y, diam, diam) 함수 사용  ]

▶ 문제 (실행결과) 
아래처럼 동작되도록 코딩하라.

▶ 프로그램(code) : 
(이미지를 클릭하면 확대 됩니다)

int diam = 10;           // 원의 직경 변수 선언(초기값 10 pixel)
float centerX, centerY;  // 원의 중심점 좌표 변수 선언

void setup() {
  size(500, 500);
  centerX = width/2;     // 화면 가운데 중심점 잡기(폭)
  centerY = height/2;    // 화면 가운데 중심점 잡기(높이)
  stroke(0);           
  strokeWeight(5);       // 선의 굵기
  fill(255, 20);             // 원의 테두리 색(255)과 내부 채움의 투명도(Alpha:20)
}
void draw() {
  background(180);     // 잔상이 남지 않도록 루프를 반복할 때 마다 배경을 새로 입힌다
  ellipse(centerX, centerY, diam, diam);
  diam += 10;          // 직경을 10pixel 씩 증가 시킨다
  if (diam == width) diam = 0;   // 원의 최대크기가 화면 사이즈를 벗어나지 않도록 리셋 시켜준다
//  diam %= width;                  // 원의 최대크기 = 화면 사이즈가 되면 나머지 값(%)이 0이 된다.
  delay(50);                           // 원이 커지는 시간지연 값
}

▶ 프로그램(code) 다운로드: 
(압축 파일을 풀어서 사용하세요)

▶ 내용설명&실행결과(영상) :
(영상을 확대하고 고화질로 보세요)

(유튜브에서 보기  : 1080p 지원)

https://youtu.be/5mQgZXo9IbY

( 카카오 : 720P 화질 지원)

【 프로세싱 기초#19 】 그림 이동하며 그리기 2

 앞선 과제에 이어, 움직이는 도형(라인)을 구현해 보려한다.  이번에는 배열이라는 요소를 사용하는데, 간단하고 효과적인 방법이므로, 잘 기억하면 좋다. 

[ 프로세싱에서의 좌표 ]

▶ 문제 1  :  선 움직이기 2
    조건 :  1. 화면 사이즈(가로x세로 픽셀) : 400 x 400) .
              2. 배경색 및 라인: background(0) . 
              3. 10개의 세로 라인을 배열을 이용하여 위치값을 주면서 그릴 것. (세로라인 그리기 : y1=0, y2=height 고정)

              4. 배열에 선의 처음 위치값을 초기 값으로 지정 해줌 (0, 40, 80, ... 360)

              5. 선의 이동할 범위를 -10~+10 사이값으로 랜덤생성시켜 적용할 것.
              6. 랜덤 값이 화면 사이즈를 벗어 나지 않도록 함(constrain (a, b, c) : a변수의 값을 b이상 c이하 값으로 함)
              7. 이동되는 느낌을 주기위해 draw() 반복 루프에, 배경을 검은색으로 줄 것 ( 'background(0)' )

▶ 실행결과 1 (동작확인):

(전체 보기, 고화질 보기로 보세요)

▶ 프로그램(code)  1: 
(이미지를 클릭하면 확대 됩니다)

float[] arrayOfPositions; // 배열 변수의 선언
void setup() {
  size(400, 400);
  background(0);
  stroke(255);  // 라인을 흰색으로
  arrayOfPositions = new float[10]; //'10'자리 배열변수 메모리할당
  // 배열변수를 초기화하는 루틴 
  for (int i=0; i<10; i+=1) {
    arrayOfPositions[i] = width/10 * i; //"0, 40, 80, ... 360" 초기 위치값 주기
  }
}
void draw()  {
  background(0);  // 배경을 검은색으로 매번 지우지(매우지) 않으면 잔상이 남는다.
  for(int i=0; i<10; i+=1) {
    arrayOfPositions[i] += int(random(-10,10));//'±10' 범위 랜덤값 적용    
    arrayOfPositions[i] = constrain(arrayOfPositions[i], 0, width);//0~width까지 한정
  }  
  for(int i=0; i<10; i+=1) {
    line(arrayOfPositions[i], 0, arrayOfPositions[i], height); //line(x1, y1, x2, y2)
  }
  delay(300);
}

▶ 프로그램(code) 다운로드 1: 
(압축 파일을 풀어서 사용하세요)

【 프로세싱 기초#18 】 그림 이동하며 그리기 

 이제까지는 박스에 색을 입히거나, 도형을 특정위치에 그리기만 해보았다. 이제 부터는 움직이는 도형을 구현해 볼 것이다. 프로세싱을 사용하는 주된 이유도 이런 동적움직임에 있다. 좀더 흥미롭고 재미가 있을 것이다. 

[ 직교 좌표계와 극좌표계 ]

▶ 문제 1  :  선 움직이기
    조건 :  1. 화면 사이즈(가로x세로 픽셀) : 400 x 400) , 
              2. 배경색 및 라인: background(0),  라인의 알파 값 (투명도: 20 )
              3. 라인이 화면 사이즈를 벗어 나지 않도록 함(constrain (a, b, c) : a변수의 값을 b이상 c이하 값으로 함)
              4. 새로운 라인을 그리면서 기존의 라인은 남겨 둘 것.(※그려진 라인을 이동시키는 것은 아님)

▶ 실행결과 1 (동작확인):

(전체 보기, 고화질 보기로 보세요)

▶ 프로그램(code)  1: 
(이미지를 클릭하면 확대 됩니다)

// x 와 y 변수는 전역변수로 선언한다

float x1, y1;  // 선의 한 쪽 끝점  
float x2, y2;  // 선의 다른 끝점 

void setup() { 
  size(400, 400); 
  background(0);   
  x1 = width/2;  
  y1 = 0; 
  x2 = width/2; 
  y2 = height;  } 
void draw()  { 
  stroke(255, 255, 255, 30); //RGB값 & 30은 투명도(Alpha) 
  x1 = x1 + random(-10, 10); //-10 이상 10 미만으로 랜덤생성 
  x2 = x2 + random(-10, 10); 
  y1 = y1 + random(-10, 10); 
  y2 = y2 + random(-10, 10); 
  // 라인이 스크린을 벗어나지 않도록 함(constrain) 
  x1 = constrain(x1, 0, width); // x1값은 0~width 사이로 고정 
  x2 = constrain(x2, 0, width); 
  y1 = constrain(y1, 0, 10); 
  y2 = constrain(y2, height-10, height); 
  line(x1, y1, x2, y2); 
  delay(50); 
}

▶ 프로그램(code) 다운로드 1: 
(압축 파일을 풀어서 사용하세요)